Option Payoff Values

An option’s payoff defines as the price an investor would be willing to pay for the option the instant before it expires.

An option’s payoff is distinct from its price or premium because the payoff only refers to the price of the option at a particular instant in time, the expiration date.

Graphs that illustrate an option’s payoff as a function of the underlying stock price are called payoff diagrams.

A payoff diagram is a valuable analytical device for understanding options. A payoff diagram graphs the payoff of an option as a function of the underlying asset’s spot price at expiration.

Payoff diagrams are extremely useful tools for understanding how options behave and how they can be combined to form portfolios with fascinating properties.

The payoff ignores the initial price that was paid for the option. Payoff treats the initial price as a sunk cost and measures only what the option owner might subsequently receive.

The payoff minus the initial price is known as the option profit. The option payoff is the same for all owners of the option, regardless of what they each initially paid for it.

Profit, however, depends on what was initially paid and therefore differs from one investor to another.

Thus, an option’s payoff is defined as the maximum amount of money the option owner would receive at expiration if she totally liquidated her position. If the option expires out of the money, the payoff is zero.

If the option expires in the money, the payoff is the amount of money received from exercising the call option and then selling the stock in the open market.

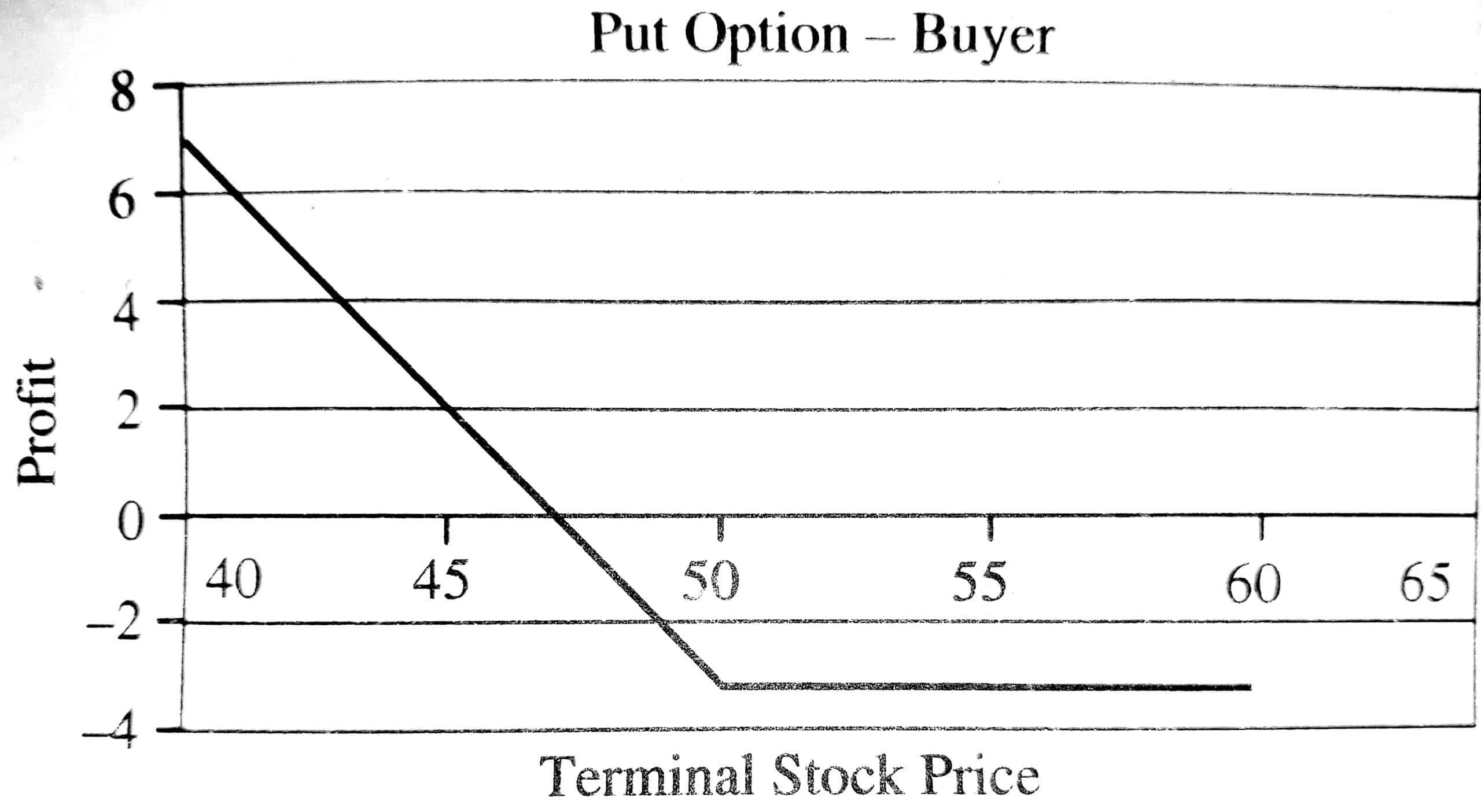
For example, suppose there is a call option that costs Rs. 3 that has an exercise price of Rs. 50. One can determine the final pay-off of the option given a variety of scenarios for the final stock price.

Since a European option can be exercised only at its expiry date, its value at expiry can be written as follows:

Call option Gr = max [0; (St – X)]
Put option PT = max [0; (X – St]

Final Stock Price	40	45	49	50	51	55	60
Terminal Pay-Off	0	0	0	0	1	5	10
Net Profit/Loss	-3	-3	-3	-3	-2	2	7

The pay-off of an option is gross of the premium paid by the buyers and received by sellers when the positions were initiated.

The net profit takes into account the premium paid by the purchaser to the writer of the option.

Figures given below show the pay-offs and profits, at exercise, for long positions and short positions, respectively.

In each case, the horizontal axis represents the asset price, S, at the date of exercise. For European options, this date must be T, the expiry date.

For American options, it is any date before or on the expiry date.

The pay-off for an option seller is the opposite of the pay-off to an option buyer. For the call option seller, the potential loss is theoretically unlimited.

For a put option seller, the maximum loss that can be incurred is the exercise price, X (if the security price falls to zero), as shown in the figures below.

Table: Obligations and Rights of Options Buyers and Sellers 

Option	Buyer	Seller
Call Option	The buyer decides whether and when an option will be exercised. Exercise occurs if St > X If option is exercised, the buyer.   Pays X Acquired the security Profit = St – X	Counter-party decides whether the option is exercised. Exercise occurs if St > X. If the option is exercised, the seller.   Receives X Delivers the asset Loss = – (X-St)
Put Option	The buyer decides whether and when an option will be exercised. Exercise occurs if St < X If option is exercised, the buyer.   Receives X Deliver the Security Profit = X-St	Counter-party decides whether the option is exercised. Exercise occurs if St < X. If the option is exercised, the seller.   Pays X Acquire the Security Loss = -(X-St)

Example: SBI shares are selling on January 1 at Rs. 2,500. Call options are available on SBI shares with expiry on January 29 and an exercise price of Rs. 2,600.

These options are priced at Rs. 70. The contract size is 132. These are American options, and these options are not expected to pay any dividends during January.

1. At what share price on January 29 would you exercise these call options?
2. Would you exercise these call options if the share price on January 17 is Rs. 2,640?
3. Calculate the terminal value of these call options (in terms of per share) for SBI share prices of Rs. 2,400, Rs. 2,500, Rs. 2,600, Rs. 2,7O0 and Rs. 2,800.
4. Calculate the gains and losses for the call buyer if SBI share prices of Rs. 2,400, Rs. 2,500, Rs. 2,600, Rs. 2,700, and Rs. 2,800.
5. Calculate the gains and losses for the call writer if SBI share prices of Rs. 2,400, Rs. 2,500, Rs. 2,600, Rs. 2,700, and Rs. 2,800.

Solution:

1. Since the exercise price of the call option is Rs. 2,600, the call option will be exercised only if the SBI share price is more than Rs. 2,600.

2. Since SBI is not expected to pay dividends during January, the option price on January 17 would be more than its in-the-money value of Rs. 40.

Therefore, it is better to sell the option rather than exercise the option. Thus the option will not be exercised on January 17.

3. The terminal values of call are shown below:

Terminal Share Price	Action	Terminal Value of Option
2,400	Do not exercise	0
2,500	Do not exercise	0
2,600	Exercise/Do not exercise	0
2,700	Excercise	100
2,800	Do not exercise	200

4. Gain to Call Buyer: Since the contract size is 132, the gain will have to be calculated for 132 shares.

Gain for the call buyer is (-132 X call premium) if the call is not exercised and [(Share price – Exercise price – Call premium) x 132] if call exercised.

Terminal Share Price	Action	Gain
2,400	Do not exercise	-132 x 70 = -9,240
2,500	Do not exercise	-132 x 70 = -9,240
2,600	Exercise/Do not exercise	-132 x 70 = -9,240
2,700	Excercise	132 x (2,700-2,600-70)=3,960
2,800	Exercise/Do not exercise	132 x (2,800-2,600-70)=17,160

5. Gain to Call Writer: Since the contract size is 132, the gain will have to be calculated for 132 shares.

Gain for the call writer is (132 x call premium) if the call is not exercised and – [(Share price – Exercise price – Call premium) x 132] if the call is exercised.

Terminal Share Price	Action	Gain
2,400	Do not exercise	132 x 70 = 9,240
2,500	Do not exercise	132 x 70 = 9,240
2,600	Exercise/Do not exercise	132 x 70 = 9,240
2,700	Excercise	-132 x (2,700-2,600-70)= -3,960
2,800	Excercise	-132 x (2,800-2,600-70)= -17,160

Payoff of Long and Short Put

The payoff of a long and short put can be explained by the example of buying and selling a put.

Buying a Put
Consider the input as follows:
Asset price today = Rs. 120
Strike price = Rs. 125
Put premium = Rs. 4

The payoff from buying a put is given in the table given below:

If End Asset Price is	Gain from Exercising Put	Premium Paid	Net Gain
117	8	-4	4
118	7	-4	3
119	6	-4	2
120	5	-4	1
121	4	-4	0
122	3	-4	-1
123	2	-4	-2
124	1	-4	-3
125	0	-4	-4
126	0	-4	-4
127	0	-4	-4
128	0	-4	-4
129	0	-4	-4
130	0	-4	-4
131	0	-4	-4
132	0	-4	-4
133	0	-4	-4
134	0	-4	-4
135	0	-4	-4
136	0	-4	-4

The buyer of a put will gain whenever the price of the asset ends up below the strike price.

However, since the buyer has to pay the premium, the gains will arise only after the premium amount has been recovered.

If the asset price ends up above the exercise price, the buyer will discard the put, resulting in a loss of the premium amount paid.

The buyer of an American put can exercise this right at any time during the tenure of the contract.

Thus, die maximum loss that the buyer can incur is only the premium amount. The asset value cannot be negative, and the lowest it can reach is only 0.

In such an eventuality, the buyer will get again equalling strike price – 0. Hence, the maximum gain that the buyer can get is the strike price.

Selling a Put

The seller of a put will gain whenever the price of the asset ends up above the strike price.

The initial premium gained by the seller will be his total gain in such circumstances.

However, if the price of the asset falls below the strike price, the seller will suffer losses.

The premium initially received will offset the losses for a small extent, but as the price ends up lower, the seller’s losses are greater.

The seller of an American call is exposed to this risk at any time during the tenure of the contract.

Thus, the maximum loss that the seller can incur is the strike price (since the asset value cannot go below 0), while the maximum profit will be the premium received.

For the following inputs, the payoff from selling a put is given in the table given below:

Input
Asset price today = Rs. 120
Strike price = Rs. 125
Put premium = Rs. 4

End Asset Price	Loss from Put Being Exercising	Premium Received	Net Gain
117	-8	4	-4
118	-7	4	-3
119	-6	4	-2
120	-5	4	-1
121	-4	4	0
122	-3	4	1
123	-2	4	2
124	-1	4	3
125	0	4	4
126	0	4	4
127	0	4	4
128	0	4	4
129	0	4	4
130	0	4	4
131	0	4	4
132	0	4	4
133	0	4	4
134	0	4	4
135	0	4	4
136	0	4	4

Payoff of Long and Short Call

The payoff of long and shortfall can be explained by the example of buying and selling a call.

Buying a Call
Consider the following input:
Asset price today = Rs. 120
Strike price = Rs. 125
Call premium = Rs. 4

We need to buy a call. The payoff from buying a call is given in the table given below:

End Asset Price	Gain from Put Being Exercising	Premium paid	Net Gain
120	0	-4	-4
121	0	-4	-4
122	0	-4	-4
123	0	-4	-4
124	0	-4	-4
125	0	-4	-4
126	1	-4	-3
127	2	-4	-2
128	3	-4	-1
129	4	-4	0
130	5	-4	1
131	6	-4	2
132	7	-4	3
133	8	-4	4
134	9	-4	5
135	10	-4	6
136	11	-4	7
137	12	-4	8
138	13	-4	9
139	14	-4	10
140	15	-4	11

The buyer of a call will gain whenever the price of the asset exceeds the strike price.

However, since the buyer has to pay the premium, the gains will arise only after the premium amount has been recovered beyond the exercise price.

If the asset price ends up below the exercise price, the buyer will discard the call, resulting in a loss of the premium amount paid.

The buyer of an American call can exercise this right at any time during the tenure of the contract.

Thus, the maximum loss that the buyer can incur is only the premium amount. While the maximum profit can be infinite.

Selling a Call

The seller of a call will gain whenever the price of the asset ends up below the strike price. The initial premium gained by the seller will be his total gain in such circumstances.

However, if the price of the asset exceeds the strike price, the seller will suffer losses.

The premium initially received will offset the losses for a small extent, but as the price ends up higher, his losses are greater.

The seller of an American call is exposed to this risk at any time during the tenure of the contract.

Thus, the maximum loss that the seller can incur is infinite, while the maximum profit will be the premium received.

This can be understood considering the following:

Input

Stock price = Rs. 120, Strike price = Rs. 125, Call premium = Rs. 4

In the above situation, if a call is written with a strike price of Rs. 125, the payoff under various scenarios is depicted in the table given below:

End Asset Price	Gain from Put Being Exercising	Premium paid	Net Gain
121	0	4	4
122	0	4	4
123	0	4	4
124	0	4	4
125	0	4	4
126	-1	4	3
127	-2	4	2
128	-3	4	1
129	-4	4	0
130	-5	4	-1
131	-6	4	-2
132	-7	4	-3
133	-8	4	-4
134	-9	4	-5
135	-10	4	-6
136	-11	4	-7
137	-12	4	-8
138	-13	4	-9
139	-14	4	-10
140	-15	4	-11