There are several different ways to price futures contracts. Fortunately, all lead to the same fair price for a given contract. Each approach relies on the law of one price.
This law states that a given financial asset (or liability) must have the same price regardless of the means by which one goes about creating that asset (or liability).
Demonstrate one way in which futures contracts can be combined with cash market instruments to create cashflows that are identical to other cash securities.
The law of one price implies that the synthetically created cash securities must have the same price as the actual cash securities.
Similarly, cash instruments can be combined to create cashflows that are identical to futures contracts.
By the law of one price, the futures contract must have the same price as the synthetic futures created from cash instruments.
The theoretical futures price may be at a premium to the cash market price (higher than the cash market price) or at a discount from the cash market price (lower than the cash market price), depending on the value of (r — c).
The term r — c is called the net financing cost because it adjusts the financing rate for the coupon interest earned.
The net financing cost is more commonly called the cost of carry or simply carry. Positive carry means that the current yield earned is greater than the financing cost; negative carry means that the financing cost exceeds the current yield. The relationships can be expressed as follows:
| Carry | Futures Price |
| Positive ( c > r ) | Will sell at a discount to the cash price ( F < P ) |
| Negative ( c < r ) | Will sell at a premium to the cash price ( F> P ) |
| Zero ( r = c ) | Will be equal to the cash price ( F= P ) |
The following sections examine the pricing relationships for a number of futures contracts.
Perishable Commodities
Perishable commodities offer the exception to the rule that futures contracts are priced on the basis of arbitrage since the commodity has to be storable for arbitrage to be feasible.
On a perishable futures contract, the futures price will be influenced by:
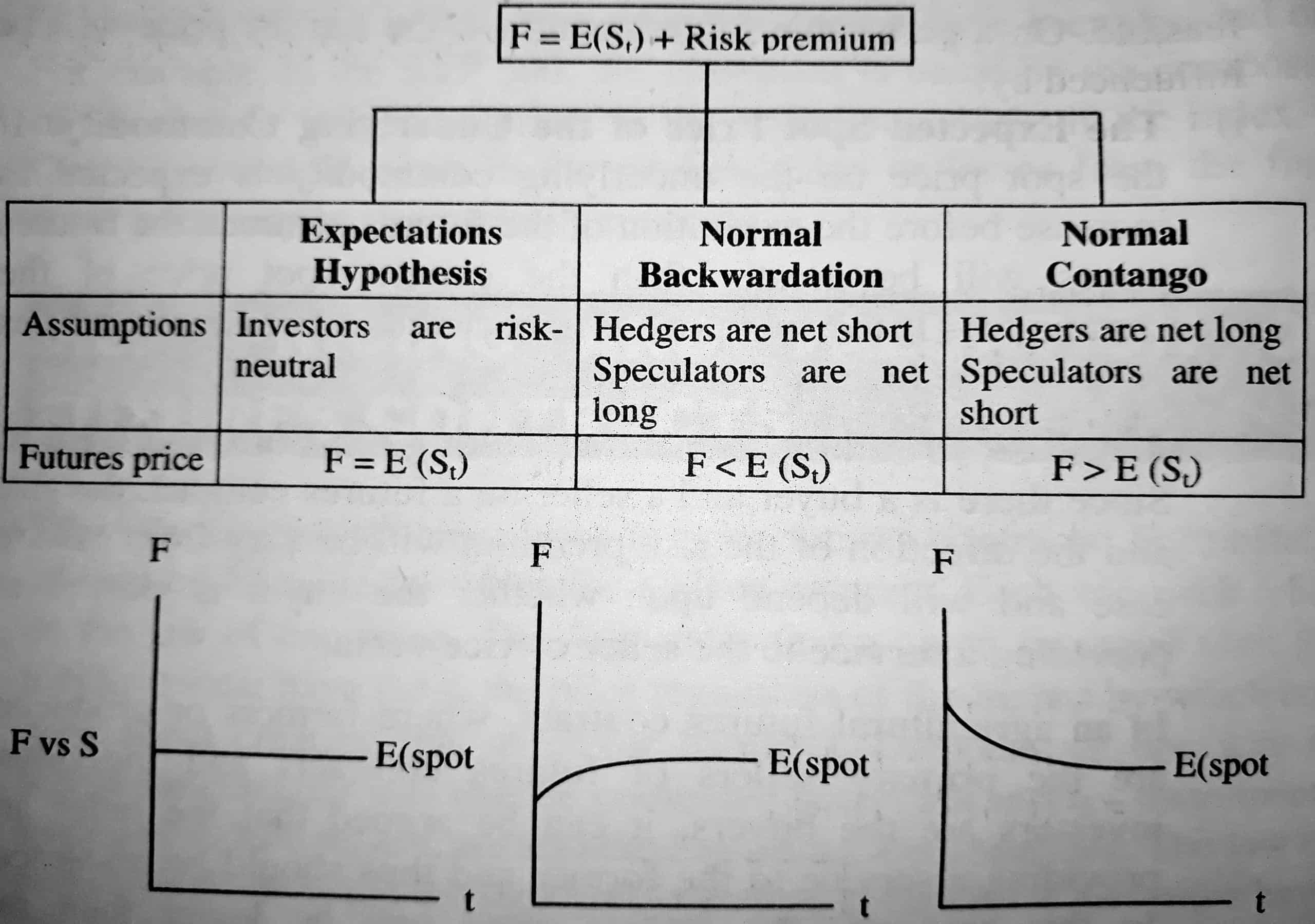
i. The Expected Spot Price of the Underlying Commodity: If the spot price on the underlying commodity is expected to increase before the expiration of the futures contract, the futures prices will be greater than the current spot price of the commodity. If the spot price is expected to decrease, the futures price will be lower than the spot price.
ii. Any Risk Premium Associated Taking the Futures Position: Since there is a buyer and a seller on a futures contract, the size and the direction of the risk premium will vary from case to case and will depend upon whether the buyer is viewed as providing a service to the seller or vice versa.
In an agricultural futures contract, where farmers or producers are the primary sellers of futures contracts and individual investors are the buyers, it can be argued that the latter is providing a service to the former and thus should be rewarded.
In this scenario, the futures price will be lower than the expected spot price.
Futures price = Spot Price – Expected Risk Premium
In this type of relationship between futures and spot prices, prices are said to exhibit ‘normal backwardation’.
In a futures contract, where buyers of the futures contract are industrial users (a good example would be Hershey’s, a chocolate manufacturer, buying sugar futures to lock in favorable prices) and the sellers are individual investors, the buyers are being provided the service and the sellers could demand a reward, leading to a risk premium that is positive.
In this case, the futures price will be greater than the expected spot price (assuming flat expectations) and futures prices are said to exhibit ‘normal contango’.
In most modem commodity futures markets, neither sellers nor buyers are likely to be dominated by users or producers, and the net benefit can accrue to either buyers or sellers and there is no a priori reason to believe that risk premiums have to be positive or negative.
In fact, if buyers and sellers are both speculating on the price, rather than hedging output or input needs, the net benefit can be zero, leading to a zero risk premium. In such a case the futures price should be equal to the expected spot price
Storable Commodities
The distinction between storable and perishable goods is that storable goods can be acquired at the spot price and stored till the expiration of the futures contract, which is the practical equivalent of buying a futures contract and taking delivery at expiration.
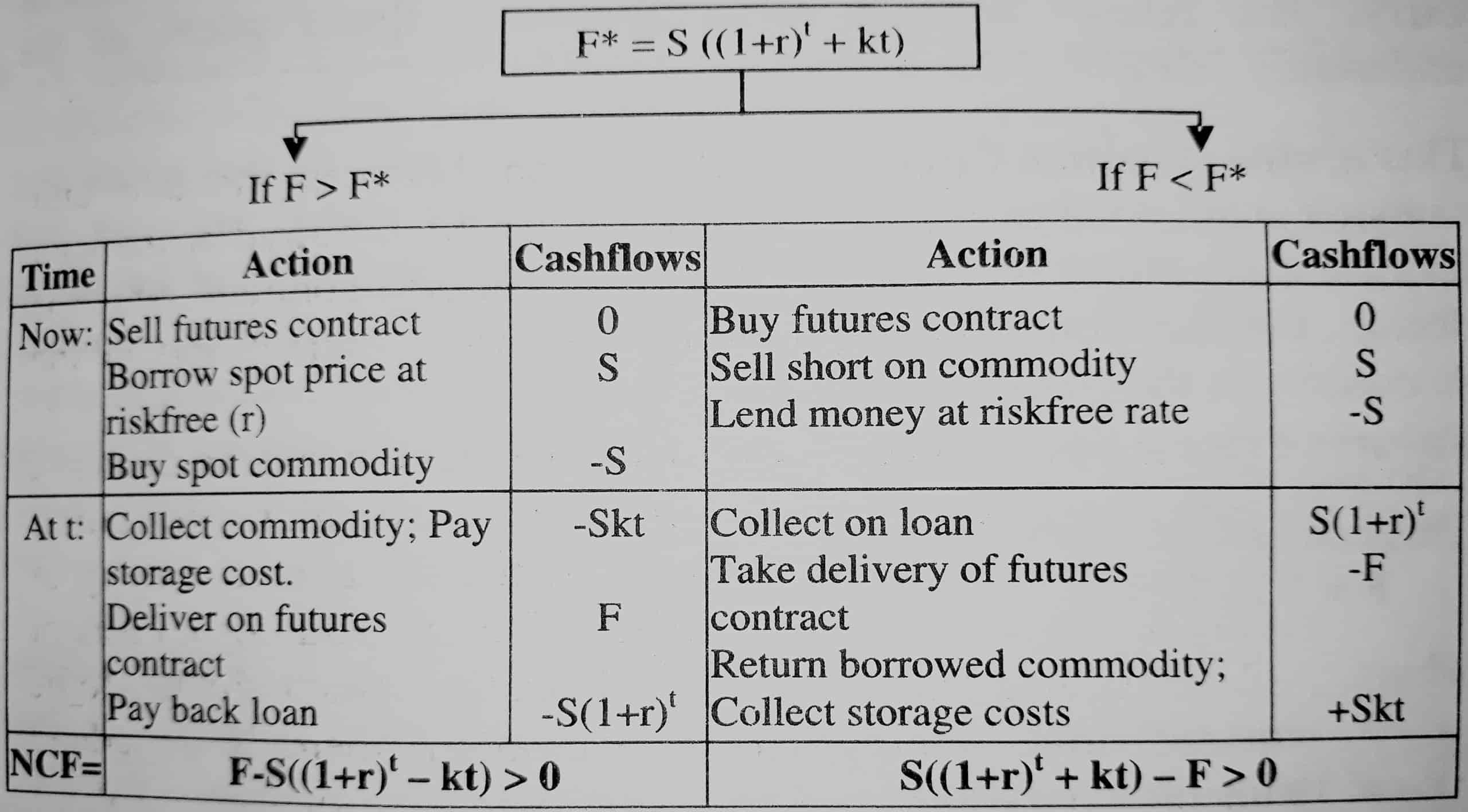
i. Since the two approaches provide the same result, in terms of having possession of the commodity at expiration, the futures contract, if priced right, should cost the same as a strategy of buying and storing the commodity.
The two additional costs of the latter strategy are as follows. Since the commodity has to be acquired now, rather than at expiration, there is an added financing cost associated with borrowing the funds needed for the acquisition now.
Added Interest Cost (Spot price) ( 1 + Interest Rate) Life of Futures contract -1
ii. If there is a storage cost associated with storing the commodity until the expiration of the futures contract, this cost has to be reflected in the strategy as well.
In addition, there may be a benefit to having physical ownership of the commodity. This benefit is called the convenience yield and will reduce the futures price.
The net storage cost is defined to be the difference between the total storage cost and the convenience yield.
If F is the futures contract price, S is the spot price, r is the annualized interest rate, t is the life of the futures contract and k is the net annual storage costs (as a percentage of the spot price) for the commodity, the two equivalent strategies and their costs can be written as follows.
Strategy 1: Buy the futures contract. Take delivery at expiration. Pay $F.
Strategy 2: Borrow the spot price (S) of the commodity and buy the commodity. Pay the additional costs.
- Interest cost
- Cost of storage, net of convenience yield = Skt
If the two strategies have the same costs,
F* = S [ (1+r)t – 1]
= S [ (1+r)t – 1] + Skt
= S [ (1+r)t -1 ] + kt